This is not reasoning

🥝 LLMs caught cheating at a math test

How do you check if an LLM is good at math?

We could just give it a bunch of math problems and see if the model can solve them. Put in a math puzzle, check the answer, repeat.

Example puzzle: Oliver picks 44 kiwis on Friday. Then he picks 58 kiwis on Saturday. On Sunday, he picks double the number of kiwis he did on Friday. How many kiwis does Oliver have?

Large language models are doing well on this type of testing. The leading models easily beat 90% success rate on GSM8K, a standard data set of grade school (age 11 to 14) math problems.

So that settles it, LLMs can reliably do grade school math, right?

Unless, of course, they are cheating.

What’s “cheating”

It’s cheating if the student submits what is a correct answer, but without actually exercising the reasoning capabilities needed to find it.

Humans cheat on a math test by copying the answer of their neighbor. Or, if the teacher is using the same test for multiple groups, by memorising the answer before the test.

What if the student mechanically replicates the structure of an answer they saw before, without understanding the logic of it? If that’s enough to pass the exam, we’d say that the teacher needs to improve their tests.

It turns out that it’s exactly what’s happening with LLMs and grade school math benchmarks.

The Apple paper

In a recent paper, Apple researchers wanted to answer this question: are LLMs capable of actual mathematical reasoning? Or are they just parroting the patterns they saw in the training data, like a student mechanically and correctly responding to a math question they don’t actually understand.

To test this, they did what a human teacher would do to challenge the understanding of their students. They added a bunch of irrelevant statements to the math puzzles.

For example, they transformed this simple puzzle:

Oliver picks 44 kiwis on Friday. Then he picks 58 kiwis on Saturday. On Sunday, he picks double the number of kiwis he did on Friday. How many kiwis does Oliver have?

Into

Oliver picks 44 kiwis on Friday. Then he picks 58 kiwis on Saturday. On Sunday, he picks double the number of kiwis he did on Friday, but five of them were a bit smaller than average. How many kiwis does Oliver have?

How did LLMs do on the updated data set?

Results

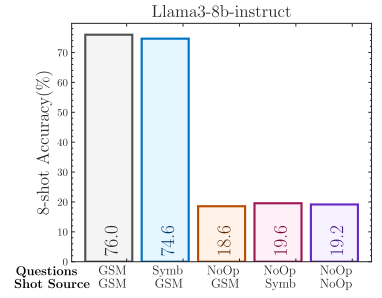
LLMs can’t tell that smaller kiwis are still kiwis.

In the chart above, we see Llama3-8b go from 76% success rate on the original puzzle set (GSM) to just 19% success rate on the puzzles modified with irrelevant statements (NoOp).

This seems to be consistent across all leading models:

By adding seemingly relevant but ultimately irrelevant information to problems, we demonstrate substantial performance drops (up to 65%) across all state-of-the-art models.

Conclusion

LLM responses can appear very convincing: the models are linguistically fluent.

But there’s no formal reasoning behind each answer. The models rehash relevant information from their training data set. When constructing the answer, they follow learned approximations of meaning and context, not logic.

Fluency doesn’t equal comprehension.

More on this

Gary Marcus says I told you so.

Symbol manipulation, in which some knowledge is represented truly abstractly in terms of variables and operations over those variables, much as we see in algebra and traditional computer programming, must be part of the mix. Neurosymbolic AI — combining such machinery with neural networks – is likely a necessary condition for going forward.

Postcard from Paris

I went to see some of my theater teachers perform in an improv-based show Aléas. Amazing what true professionals can do on a stage 🤩.

There’s no script for life so all what we do is improv :).

Keep going,
– Przemek